How do I test my data for normality?
Before applying statistical methods that assume normality, it is necessary to perform a normality test on the data.
For example, all of the following statistical tests, statistics, or methods assume that data is normally distributed:
- Hypothesis tests such as t tests, Chi-Square tests, F tests
- Analysis of Variance (ANOVA)
- Least Squares Regression
- Control Charts of Individuals with 3-sigma limits
- Common formulas for process capability indices such as Cp and Cpk
Before applying statistical methods that assume normality, it is necessary to perform a normality test on the data (with some of the above methods we check residuals for normality). We hypothesize that our data follows a normal distribution, and only reject this hypothesis if we have strong evidence to the contrary.
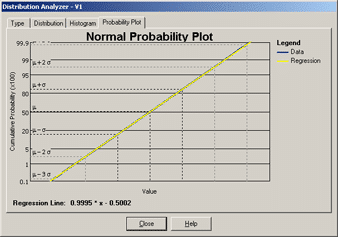
Figure 2: Normal probability plot illustrating normal distribution
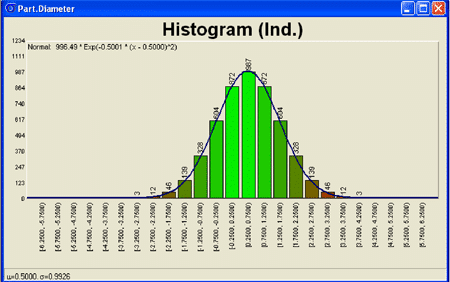
While it may be tempting to judge the normality of the data by simply creating a histogram of the data, this is not an objective method to test for normality – especially with sample sizes that are not very large. With small sample sizes, discerning the shape of the histogram is difficult. Furthermore, the shape of the histogram can change significantly by simply changing the interval width of the histogram bars.
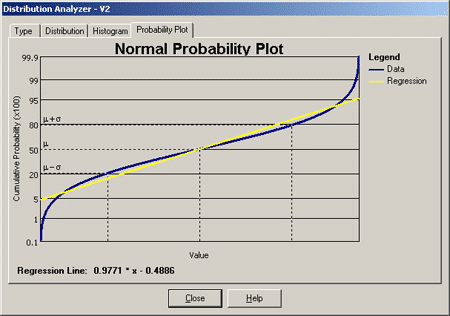
Normal probability plotting may be used to objectively assess whether data comes from a normal distribution, even with small sample sizes. On a normal probability plot, data that follows a normal distribution will appear linear (a straight line). For example, a random sample of 30 data points from a normal distribution results in the first normal probability plot (Figure 2). Here, the data points fall close to the straight line. The second normal probability plot (Figure 3) illustrates data that does not come from a normal distribution.
Many methods are available to handle non-normal data and these should be utilized when necessary. Applying methods which assume the normal distribution when this assumption is not valid often results in incorrect conclusions.



Recent Comments